The Plank's Constant in Action

Maybe you already heard about Plank's constant, but you wonder what it is all about. How it was discovered and how it is applied and what Physics that this constant is applied to, but before we dive into the details let us first learn who discovered it and what is the reason why this number is determined. 

Let us go back in history. In the late 19th century, physicists were puzzled by the mysterious behavior of blackbody radiation. A blackbody is an idealized physical object that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. In simpler terms, it is a perfect absorber and emitter of radiation. When a blackbody is heated, it emits radiation in a characteristic spectrum that depends only on its temperature, not on its material or surface properties. A blackbody, as described in physics, is an idealized concept rather than a real, physical object. It's a theoretical model used to understand how objects absorb and emit radiation. 

Despite their best efforts, existing theories couldn't explain why the spectrum of radiation emitted by a blackbody didn't match their predictions. Enter Max Planck, a German physicist with a bold idea. In 1900, Planck proposed that energy wasn't emitted or absorbed continuously, as everyone had believed, but in discrete packets he called "quanta." This radical hypothesis led him to derive a new formula, now known as Planck's law, which accurately described the blackbody radiation spectrum. Central to this formula was a new constant, h, which we now know as Planck's constant. This discovery was groundbreaking, laying the foundation for quantum mechanics and forever changing our understanding of the microscopic world. For his revolutionary work, Planck was awarded the Nobel Prize in Physics in 1918, cementing his place in the annals of scientific history.

Energy wasn't emitted or absorbed continuously, but in discrete packets he called "quanta."

 Planck's constant, approximately \( h = 6.626 \times 10^{-34} \, \text{Js}\) is a fundamental quantity in quantum mechanics that plays a crucial role in our understanding of the microscopic world. This tiny number is central to the equation \(E = h \nu \), which relates the energy of a photon to its frequency, showing that energy is quantized and comes in discrete packets rather than a continuous flow, where E is the energy, h is the Planck's constant, and \( \nu \) is the frequency of the photon.

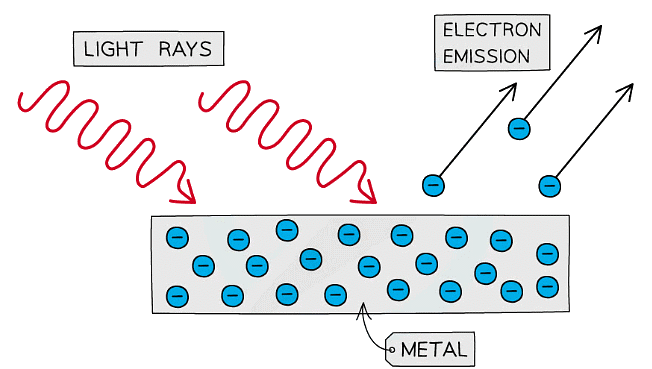
We know that photons exhibit both wave-like and particle-like properties, a concept known as wave-particle duality. When two or more waves overlap, they can interfere with each other, creating patterns of constructive and destructive interference (Interference) and photons can bend around obstacles and spread out after passing through small openings, similar to how water waves behave (diffraction). Photons also exhibit particle-like properties, when photons hit a material, they can transfer energy to electrons, causing them to be ejected from the material. This effect supports the idea that photons have discrete energy packets (quanta). This effect is called photoelectric effect. On the other hand, the energy of a photon is quantized and given by \(E = h \nu \).

To understand more the Photoelectric effect, watch this video.

In a solar panel, the absorption of energy is a fundamental process that converts sunlight into electricity. Here's how it works:

When sunlight strikes the solar panel, it is absorbed by semiconductor materials, typically silicon. The energy from the sunlight excites electrons in the silicon atoms, causing them to jump to higher energy levels. This creates electron-hole pairs, where an electron is knocked loose from its atom, leaving behind a "hole" or positive charge.

These free electrons and holes are then separated by an electric field within the solar cell, which is created by the junction between two different types of silicon (n-type and p-type). The electric field pushes the electrons towards the n-type layer and the holes towards the p-type layer, generating a flow of electric current.

This current is collected by metal contacts on the top and bottom of the solar cell and can be used to power electrical devices or stored in batteries for later use. The entire process, from the absorption of sunlight to the generation of electric current, is known as the photovoltaic effect.

When an electron absorbs energy from any source, such as light or heat, it can reach a threshold where it becomes excited and jumps to a higher energy level within an atom. This process is known as excitation. The electron remains in this excited state temporarily. When it returns to a lower energy level, it releases the excess energy in the form of a photon, a particle of light. This emission of a photon is a key principle behind phenomena like fluorescence and the operation of lasers. The energy of the emitted photon corresponds to the difference between the higher and lower energy levels of the electron. 

This revolutionary idea helped explain phenomena like blackbody radiation and the photoelectric effect. Planck's constant is a cornerstone of quantum mechanics, appearing in many fundamental equations, such as the Schrödinger equation, and setting the scale at which quantum effects become significant. Its small value means that quantum effects are typically noticeable only at very small scales, such as atoms and subatomic particles, while classical physics dominates at larger scales. The introduction of Planck's constant marked the beginning of quantum theory, revolutionizing physics, chemistry, and many other fields, and leading to the development of technologies like semiconductors, lasers, and quantum computers. Despite its small size, Planck's constant has had an immense impact on science and technology.

Take the quiz if you are ready. If you don't have the access code, get your access code from the link, input your students ID number without dash (-).

TAKE THE QUIZ GET ACCESS CODE HERE