Understanding Thermal Equilibrium and Its Connection to Spectral Density of Electromagnetic Radiation

Learning Objectives

• Define Thermal Equilibrium: Explain the concept of thermal equilibrium and describe the conditions under which it occurs.
• Understand Energy Distribution: Articulate how energy is distributed in a system at thermal equilibrium, using examples such as a hot cup of coffee cooling down in a room.
• Connect to Spectral Density: Describe the relationship between thermal equilibrium and the spectral density of electromagnetic radiation, particularly in the context of black bodies.
• Apply Planck's Law: Explain how Planck's law governs the emission of radiation from objects in thermal equilibrium and how this relates to temperature and wavelength.

Thermal equilibrium occurs when two or more objects or systems in contact with each other reach the same temperature, and there is no net flow of heat between them. Essentially, it's a state where the temperature is uniform throughout the system, and energy is evenly distributed.

Thermal equilibrium is when two or more objects or systems reach the same temperature, so there's no net flow of heat between them. Imagine a hot cup of coffee left in a room; eventually, the coffee cools down, and the room's air warms up slightly until both are at the same temperature. This is thermal equilibrium.

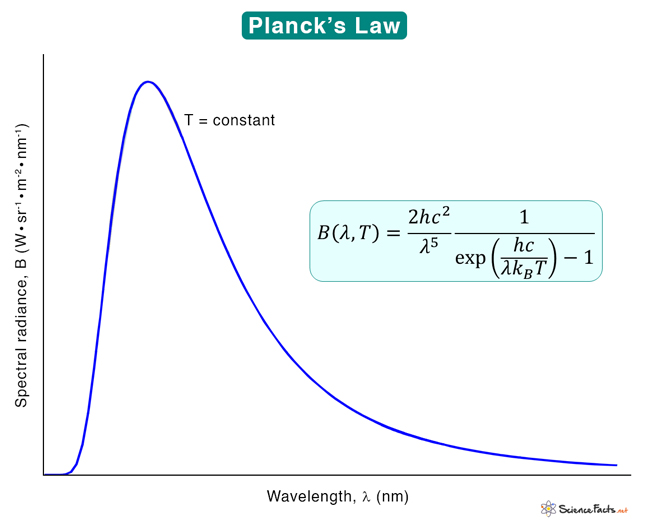
Now, let's connect this to the spectral density of electromagnetic radiation. A black body is an ideal object that absorbs all incoming light and emits radiation based on its temperature. When a black body is in thermal equilibrium, it emits radiation with a specific pattern described by Planck's law. This law tells us how much energy is emitted at different wavelengths, depending on the temperature.

The spectral density is a measure of how this energy is spread across different wavelengths. In thermal equilibrium, the energy distribution follows Planck's law, meaning it depends only on the temperature and the wavelength. This stable energy distribution helps us understand how objects radiate and absorb energy in various situations.

Let us elaborate more our simple example involving a hot cup of coffee and a room.

Imagine you have a hot cup of coffee at 80°C and you place it in a room that's at 20°C. Initially, the coffee is much hotter than the room. Over time, heat will flow from the coffee to the cooler air in the room. Eventually, the coffee and the room will reach the same temperature, say 25°C. At this point, they are in thermal equilibrium because there's no net flow of heat between them.

Now, let's connect this to the spectral density of electromagnetic radiation. Suppose the coffee cup and the room are ideal black bodies. When they reach thermal equilibrium at 25°C, they will emit radiation according to Planck's law. This law describes how the energy is distributed across different wavelengths. For example, at 25°C, the black bodies will emit more infrared radiation than visible light.

According to Planck's law, at any given temperature, a black body emits radiation across a wide range of wavelengths, forming a continuous spectrum. However, the intensity of the radiation is not uniform across all wavelengths.

The spectral density tells us how much energy is emitted at each wavelength. In thermal equilibrium, the energy distribution follows Planck's law, meaning it depends only on the temperature and the wavelength. This stable energy distribution helps us understand how objects radiate and absorb energy in various situations.

So, in this example, thermal equilibrium ensures that the coffee cup and the room emit radiation in a predictable pattern based on their shared temperature, following Planck's law.

Wien's Displacement Law

Since the temperature changes overtime as it reaches thermal equilibrium, the energy of radiation also changes proportionally. That means if the temperature increases the energy emitted by the hot object is also increasing. The radiation happened through an electromagnetic wave, we already understood that once a greater energy is emitted by a shorter wavelength. This means that if the temperature decreases the wavelength of the radiation emitted will increase. So, temperature and wavelength have inverse proportionality.  In Wien's displacement law, we use lambda ( \( \lambda \) ) to represent the wavelength. Take note the smaller the wavelength the higher the energy it carries. 

Wien's Displacement Law

Wien's displacement law states that the wavelength at which the emission of a black body spectrum is maximized is inversely proportional to the temperature of the black body. The law is given by:

\[ \lambda_{\text{max}} = \frac{b}{T} \]

where:

• \( \lambda_{\text{max}} \) is the peak wavelength.
• \( b \) is Wien's displacement constant (\( b \approx 2.897 \times 10^{-3} \) m·K).
• \( T \) is the absolute temperature of the black body.

This law states that the peak wavelength of the radiation emitted by a black body is inversely proportional to its temperature. In other words, as the temperature of the black body increases, the peak wavelength of the emitted radiation shifts to shorter wavelengths.

Image Source: Planck’s Law: Statement and Formula

Planck's Law Calculation

Problem:

Calculate the spectral radiance of a blackbody at a temperature of 5000 K at a frequency of \( 5 \times 10^{14} \) Hz using Planck's law.

Solution:

$$ B(\nu, T) = \frac{2h\nu^3}{c^2} \cdot \frac{1}{e^{\frac{h\nu}{kT}} - 1} $$

Given:

• Planck's constant (\( h \)) = \( 6.626 \times 10^{-34} \) J·s
• Speed of light (\( c \)) = \( 3 \times 10^8 \) m/s
• Frequency (\( \nu \)) = \( 5 \times 10^{14} \) Hz
• Boltzmann's constant (\( k \)) = \( 1.381 \times 10^{-23} \) J/K
• Temperature (\( T \)) = 5000 K

Plugging in the values:

$$ B(5 \times 10^{14} \, \text{Hz}, 5000 \, \text{K}) = \frac{2 \times 6.626 \times 10^{-34} \, \text{J·s} \times (5 \times 10^{14} \, \text{Hz})^3}{(3 \times 10^8 \, \text{m/s})^2} \cdot \frac{1}{\exp\left(\frac{6.626 \times 10^{-34} \, \text{J·s} \times 5 \times 10^{14} \, \text{Hz}}{1.381 \times 10^{-23} \, \text{J/K} \times 5000 \, \text{K}}\right) - 1} $$

Simplifying the exponent:

$$ \frac{6.626 \times 10^{-34} \, \text{J·s} \times 5 \times 10^{14} \, \text{Hz}}{1.381 \times 10^{-23} \, \text{J/K} \times 5000 \, \text{K}} \approx 4.78 $$

So the spectral radiance is:

$$ B(5 \times 10^{14} \, \text{Hz}, 5000 \, \text{K}) = \frac{2 \times 6.626 \times 10^{-34} \, \text{J·s} \times (5 \times 10^{14} \, \text{Hz})^3}{(3 \times 10^8 \, \text{m/s})^2} \cdot \frac{1}{e^{4.78} - 1} $$

Calculating the denominator:

$$ e^{4.78} - 1 \approx 119.4 $$

Finally, calculating the spectral radiance:

$$ B(5 \times 10^{14} \, \text{Hz}, 5000 \, \text{K}) \approx \frac{2 \times 6.626 \times 10^{-34} \, \text{J·s} \times 1.25 \times 10^{43} \, \text{Hz}^3}{9 \times 10^{16} \, \text{m}^2/\text{s}^2} \cdot \frac{1}{119.4} $$

$$ B(5 \times 10^{14} \, \text{Hz}, 5000 \, \text{K}) \approx \frac{1.65 \times 10^{-10} \, \text{J·s} \cdot \text{Hz}^3}{9 \times 10^{16} \, \text{m}^2/\text{s}^2} \cdot \frac{1}{119.4} $$

$$ B(5 \times 10^{14} \, \text{Hz}, 5000 \, \text{K}) \approx 1.38 \times 10^{26} \, \text{W/m}^2\text{/sr/Hz} \cdot \frac{1}{119.4} $$

$$ B(5 \times 10^{14} \, \text{Hz}, 5000 \, \text{K}) \approx 1.16 \times 10^{24} \, \text{W/m}^2\text{/sr/Hz} $$

So, using this form of Planck's law, the spectral radiance at \( 5 \times 10^{14} \) Hz for a blackbody at 5000 K is approximately \( 1.16 \times 10^{24} \, \text{W/m}^2\text{/sr/Hz} \).

Planck's Law Problems

Problem 1:

Calculate the spectral radiance of a blackbody at a temperature of 3000 K at a wavelength of 700 nm using Planck's law.

Given:

(\( h \)) = \( 6.626 \times 10^{-34} \) J·s
• Speed of light (\( c \)) = \( 3 \times 10^8 \) m/s
• Wavelength (\( \lambda \)) = 700 nm = \( 700 \times 10^{-9} \) m
• Boltzmann's constant (\( k_B \)) = \( 1.381 \times 10^{-23} \) J/K
• Temperature (\( T \)) = 3000 K

Use the equation:

$$ B(\lambda, T) = \frac{2hc^2}{\lambda^5} \cdot \frac{1}{\exp\left(\frac{hc}{\lambda k_B T}\right) - 1} $$

Problem 2:

Determine the spectral radiance of a blackbody at a temperature of 6000 K at a frequency of \( 6 \times 10^{14} \) Hz using Planck's law.

Given:

• Planck's constant (\( h \)) = \( 6.626 \times 10^{-34} \) J·s
• Speed of light (\( c \)) = \( 3 \times 10^8 \) m/s
• Frequency (\( \nu \)) = \( 6 \times 10^{14} \) Hz
• Boltzmann's constant (\( k \)) = \( 1.381 \times 10^{-23} \) J/K
• Temperature (\( T \)) = 6000 K

Use the equation:

$$ B(\nu, T) = \frac{2h\nu^3}{c^2} \cdot \frac{1}{e^{\frac{h\nu}{kT}} - 1} $$

Problem 3:

Find the wavelength at which the spectral radiance of a blackbody at a temperature of 4500 K is maximized using Wien's displacement law.

Given:

• Wien's constant (\( b \)) = \( 2.897 \times 10^{-3} \) m·K
• Temperature (\( T \)) = 4500 K

Use the equation:

$$ \lambda_{\text{max}} = \frac{b}{T} $$